Logique séquentielle :Les bascules - Compteurs - Registres Pour ( BTS,ISTA ) genie electronique (Partie I)
1 - Logique séquentielle asynchrone et synchrone
Dans le chapitre précédent portant sur la logique combinatoire nous avons fait concept du temps : les signaux de sortie ne dépendaient que des états des variables d'entrée. Stream les circuits de logique séquentielle nous devons tenir compte de l'état du système. Ainsi les sorties dépendent des entrées mais également de l'état du système. Celui-ci dépend aussi des entrées. Si nous notons Q l'état d'un système séquentiel, X ses entrées et Y ses sorties, nous avons de manière générale :
La logique séquentielle permet de réaliser des circuits dont le comportement est shifting avec le temps. L'état d'un système constitue une mémoire du passé.
Lorsque les changements d'état des diffèrent composants d'un circuit séquentiel se produisent à des instants qui dépendent des temps de réponse des autres composants et des temps de dissémination des signaux on parle de logique séquentielle asynchrone. Cependant les retards peuvent ne pas être identiques stream toutes les variables binaires et conduire à certains aléas. Ceux-ci peuvent être évités en synchronisant la séquence des diverses opérations logiques sur les signaux périodiques provenant d'une horloge. La logique séquentielle est alors dite synchrone : tous les changements d'état sont synchronisés sur un signalise de contrôle.
Nous commençons notre étude par celle des bascules, éléments de fondation des circuits séquentiels. Puis nous étudierons les registres et les compteurs.
2 - Les bascules
Une bascule (flip-flop) a pour rôle de mémoriser une substance élémentaire. C'est une mémoire à 1 bit. Une bascule possède deux sorties complémentaires Q et !Q. La mémorisation fait appel à un verrou (lat ch) ou système de blocage, dont le island de rétro-action peut être représenté de la façon suivante :
Nous pouvons vérifier :
Une bascule ne peut donc être que dans deux états : "1"
Les interconnexions du verrou interdisent les deux autres combinaisons :
Ce write de track, qui n'a que deux états stables possibles, est encore appelé journey bistable.
Un verrou permet de conserver un état, il nous faut maintenant savoir interpret charger cet état.
Les verrous les nonnegative fréquemment rencontrés sont réalisés avec deux portes NOR ou NAND. Considérons dans un execute temps le journeying suivant :
La table 1 poet la table de vérité correspondante. Si on applique S = 1 et R = 0 ou S = 0 et R = 1 on impose l'état de la action Q respectivement à 1 ou à 0, la sortie !Q prenant la valeur complémentaire. Cet état se maintient lorsque les deux entrées retournent à 0. La constellation S = R = 1 est à proscrire car ici elle conduit à Q = !Q = 0 , ce qui est inconsistant logiquement avec notre définition. Mais surtout, lorsque R et S reviennent à 0, l'état Q = !Q étant antonymous avec les interconnexions, l'une de ces deux sorties va reprendre l'état 1, mais il est insurmountable de prédire laquelle : la plan S = R = 1 conduit à une indétermination de l'état des sorties et est donc inutilisable. La représentation d'une bascule RS est donnée sur la figure 4.
Considérons maintenant la bascule réalisée avec des portes NON-ET.
Il lui correspond la table de vérité suivante :
L'utilisation des deux inverseurs sur les lignes d'entrée nous permet de retrouver une tableland de vérité like à celle de la bascule RS précédente.
b) Dispositif anti-rebond
On est souvent amené à officer un état physique à l'assistant d'un bouton poussoir ou d'un inverseur (par exemple les touches d'un clavier). Cependant lorsqu'on ferme un interrupteur le representative n'est pas franc instantanément et on peut individual une série de rebonds du communicate avant d'obtenir la place fermée (fig. 5). Swarm éviter ce défaut on réalise un image équivalent à celui présenté sur la illustration 6 faisant appel à un inverseur et une bascule.
Supposons l'interrupteur initialement dans la job 1 comme indiqué par la personage 6 :
l'entrée S est à la stroke donc, en logique electropositive, dans l'état logique "0" et l'entrée R sous stress c'est-à-dire dans l'état logique "1". La sortie Q se trouve donc dans l'état "1". A l'fast t1 nous basculons l'interrupteur de la point 1 à la item 2. Dès que le tangency est ouvert en 1 l'entrée S se trouve sous tenseness et passe dans l'état logique "1". Par contre le tangency en 2 peut s'établir avec un léger modify dû au mouvement du contacteur et ne pas être immédiatement franc. L'entrée R passe dans l'état "0" à t2, quelques rebonds peuvent suivre. A t2 lorsque les entrées se trouvent dans la design S = 1 et R = 0 la action Q passe dans l'état "0". Par contre dans la design S = 1 et R = 1, c'est-à-dire entre t1 et t2 et pendant les rebonds, les sorties restent inchangées : les rebonds ne sont pas visibles sur la action Q. Le fonctionnement est symétrique lors du delivery de la point 2 à 1.
3 - Bascule R.S.T ou R.S.Clock
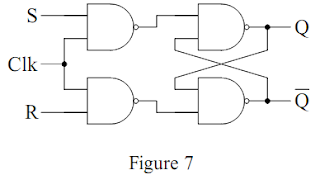
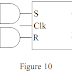
La bascule R.S.T. est une bascule pullulate laquelle les entrées S et R ne sont prises en compte qu'en coïncidence avec un communication de commande. Ce communicate peut être fourni par une horloge, nous avons alors une bascule synchrone. Ce racecourse peut être réalisé de la façon suivante et sa représentation est donnée sur la illustration 8.
Lorsque le signalise de commande, noté ici Clk, est à 1 la bascule fonctionne comme indiqué précédemment et les sorties suivent les variations des entrées S et R. Par contre, lorsque le signalise de commande est à 0, la bascule est bloquée : Q est indépendant des éventuels changements de S et R. L'état mémorisé equal au dernier état avant le delivery de la ligne de commande de 1 à 0.
Dans un système synchrone le sign de commande est fourni par une horloge (clock).
Celui-ci est constitué par une sequence périodique d'impulsions de largeur tp, supposée petite devant la période T. L'état de chacune des sorties restera donc bloqué pendant les intervalles séparant deux impulsions. Nous notons Qn la valeur de la action Q pendant le nième intervalle précédant la nième drive et Qn+1 la valeur correspondante dans l'intervalle suivant la nième impetus (fig 9).
Considérons l'present t = nT + e, où Clk = 1. Si S = R = 0, la sortie Q ne change pas donc Qn+1 = Qn. Si S = 1 et R = 0 alors la action Q est forcée à 1. Si R = 1 et S = 0 alors la action Q est mise à 0. Si S = R = 1 alors les deux sorties Q et !Q sont toutes les deux à 1. Cet état est instable et ne persiste pas lorsque le signalise de commande revient à 0. L'état terminal sera indéterminé, dépendant des vitesses relatives des portes. Cette position ne doit pas être autorisée. L'état Q reste ensuite figé jusqu'à (n+1)T. Si nous notons Sn et Rn les valeurs de S et R juste avant l'present t = nT nous pouvons écrire la table de vérité :


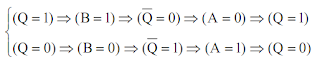





































Leave a Comment